乘法快速幂

如果需要求x^n，那么最简单的办法就是对x进行n次相乘，此时时间复杂度为O（n），而乘法快速幂可以是O（logn）的复杂度

举例

假设需要求10^75,首先对75转为二进制，为

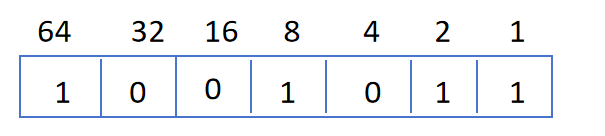
对于该例子，x=10，设置每次x = x*x

设置一个ans变量，每次有有选择地乘以x，具体选择方式如下：

x=10^1，发现1对应的二进制那一位为1，则ans = 1*x= 1*10^1

然后x=x*x，即x=10^2，发现对应的二进制那一位为1，则ans = 1*10^1*10^2

然后x=x*x，即x=10^4，发现对应的二进制那一位为0，则ans = 1*10^1*10^2，ans不变

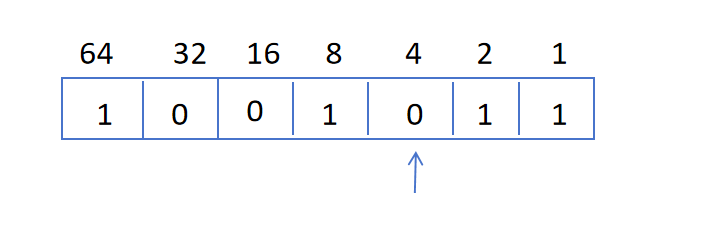
以此类推，总结下来就是先把n变成二进制，然后x每次都与自己相乘，遇到二进制对应的位为1就乘进ans里面，否则ans不动

对应的java代码如下：

 public static long power(long x, long n,long mod) {
        long res = 1;
        while (n > 0) {
            if ((n & 1)!= 0)
                res = (res * x) % mod;
            n = n >> 1;
            x = (x * x) % mod;
        }
        return res;
    }